直線近似における各パラメータの推定誤差

線形回帰のパラメータの推定

こちら，のサイトで，線形回帰の場合の各パラメータの推定を行いました．

具体的な値は，参考にしたサイトの値を使わさせていただきます．

i	x	y
1	0	5
2	2	5
3	3	7
4	4	6
5	6	9
6	9	10

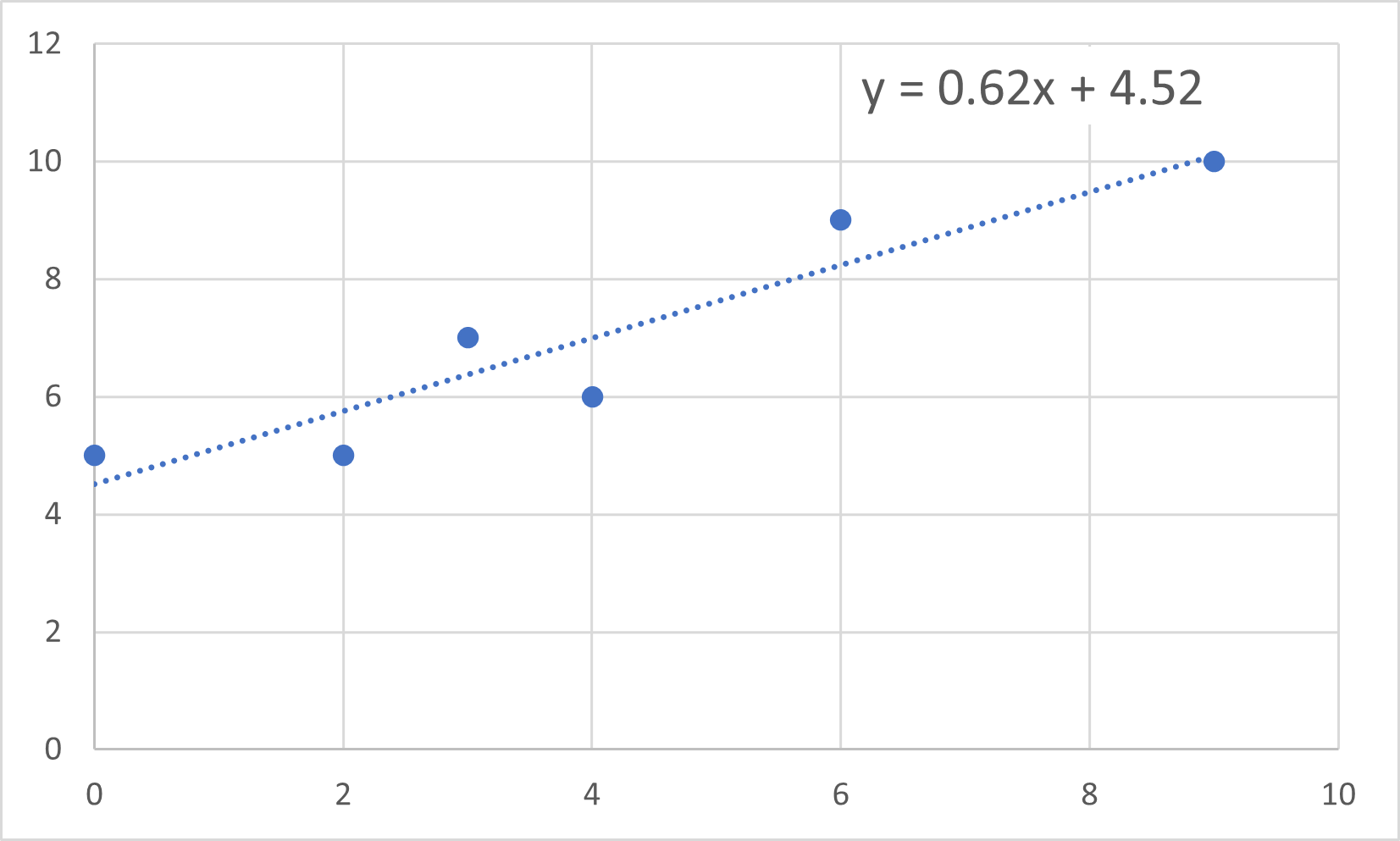
エクセルで散布図，近似曲線を描くと，

となります．

散布図からの近似曲線

エクセルでの散布図からの近似曲線では，

y = 0.62x + 4.52

となります．

真面目に計算を行って見ると，推定値は，

i	x	y	x²	xy
1	0	5	0	0
2	2	5	4	10
3	3	7	9	21
4	4	6	16	24
5	6	9	36	54
6	9	10	81	90

平均	4	7	24.33	33.17
和	24	42	146	199
平方和	146	316	8210	12133

\(\Large\displaystyle \hat{a_1} = \frac{ \overline{x y} - \bar{x} \bar{y} }
{ \displaystyle \overline{x^2}- \bar{x}^2} = \frac{ 33.17 - 4 \times 7}
{ 24.33- 4^2} = 0.62 \)

\(\Large\displaystyle \hat{a_0} = \bar{y} - \frac{ \overline{x y} - \bar{x} \bar{y} }
{ \displaystyle \overline{x^2}- \bar{x}^2} \bar{x}
= 7-0.62 \times 4 = 4.52 \)

となり，エクセルの近似結果と一致します．

回帰分析

各パラメータの推定値はこのようにエクセルでも計算できますが，各パラメータの推定誤差もエクセルから求めることができます．

それは，回帰分析，です．

　データ　→　データ分析　→　回帰分析

と進めば，

概要

回帰統計
重相関 R	0.934685
重決定 R2	0.873636
補正 R2	0.842045
標準誤差	0.833667
観測数	6

分散分析表
	自由度	変動	分散	観測された分散比	有意 F
回帰	1	19.22	19.22	27.65468	0.00626
残差	4	2.78	0.695
合計	5	22

	係数	標準誤差	t	P-値	下限 95%	上限 95%	下限 95.0%	上限 95.0%
切片	4.52	0.581578	7.771954	0.001478	2.90528	6.13472	2.90528	6.13472
X 値 1	0.62	0.117898	5.258771	0.00626	0.292662	0.947338	0.292662	0.947338

となり，各パラメータの推定誤差を計算してくれます．

	係数	標準誤差
切片	4.52	0.581578
x 値 1	0.62	0.117898

LINEST

それ以外にも，標準のエクセル関数，LINEST，でも推定誤差を計算してくれます．

　=LINEST(B2:B5, A2:A5, TRUE, TRUE)

のようなフォーマットであり，Yデータ，Xデータ，切片，追加の回帰統計

を選択します．

その結果が，

0.62	4.52
0.117898	0.581578
0.873636	0.833667
27.65468	4
19.22	2.78

となり，

行 / 列	1列目	2列目
1行目	傾き（m）	切片（b）
2行目	傾きの標準誤差	切片の標準誤差
3行目	R²（決定係数）	y の標準誤差
4行目	F値	自由度
5行目	回帰平方和	残差平方和

を示します．

次は，指数近似における決定係数，です．